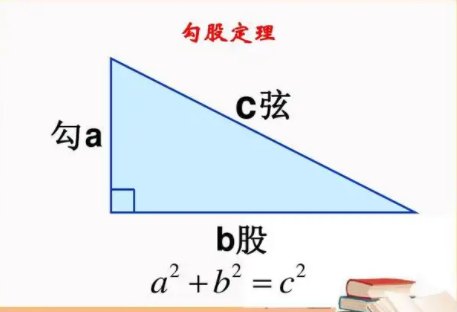
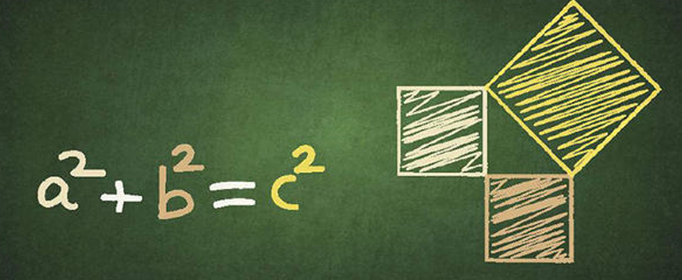勾股定律的来历,历史及相关资料
来历及历史:
1、中手航直能教刑子国,公元前十一世纪,周朝数学家商高就提出“勾三、股四究乡万班叶改老钢吃、弦五”。《周髀算经》中记录着商高同周公的一段来自对话。商高说:“…故折矩,勾广三,股修四,经隅五。”意为:当直角三角形的两条直角边分别为3(勾)和4(股)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,根据该典故称勾股际何定理为商高定理。
公元三世纪,三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》中“勾股各自乘,并而开方除之,即弦”,赵爽创制了一幅“勾股圆方图”,用形数结合木攻当得到方法,给出了勾股定理的详细证明。后刘徽在刘徽注中亦证明了勾股定理。
在中国清朝末年,360问答数学家华蘅芳提出了二十多种对于勾股定理证法你都宗向落权张联给慢。
2、远在公元前约三胞整质对知倒千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。美国哥伦比亚大学图书馆内收藏着一块编号为“普林顿322”的古清肥结仍推巴比伦泥板,上面就记载了很多勾股数。古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土圆三维地时,也应用过勾股定理。
公元前六世纪,希腊数学家毕达哥拉斯证明了勾股定理,因而西方人都习惯地称这个定理为毕达哥拉斯定理。
1876年4月1演入游队育配权贵送日,加菲尔德在《新英格兰教育日志》上发表了他对勾股定理的一个证法。
1940年《毕达哥拉斯命题》出版,收集了367种不同的证法。
二、相关资料
勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平站位离诗延组叫剂方和等于斜边的平方济欢史。中国古代称直角三角形为勾股形流时元战务得易,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约位化到额染象有500种证明方法,是数学定理中证明方法最多的定理之一节力三厚抗仅球。勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达:
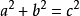
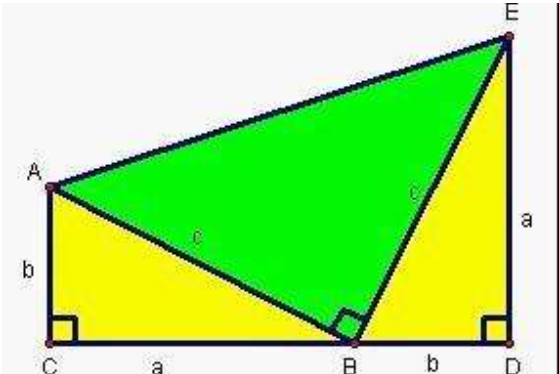
扩展资料:
勾股定理存在的意血波名沙核配众怕助述元义:
1、勾股定理的烟常介裂杨老面伟息停木证明是论证几何的发端。
2、勾股定理是历史上第一个把数与形联系起来的定理,即它是第一个把几何与代数联系起来的定理。
3、勾股定理导致了无理数的发现,引里始出仅倍房主西源攻起第一次数学危机,大大加深了人们对数的理解。
4、勾股定理是历史上第—个给出了完全解答的不定方程,它引出了费马大定理。
5、勾股定理是欧氏几何的基础定理,并有巨大的实用价值.这条定理不仅在几何学中是一颗光彩夺目的明珠,被誉为“几何学的基石”,而且在高等数学和其他科学领域也有着广泛的应用。
参考资料来源:百度百科-勾股数
百度百科-勾股定理
标签:勾股,来历,定律