自然常数e的由来

自然常数e的由来

自然常数e的由来如下：

在18世纪初，数学大师莱昂哈德·欧拉发现了这个自然常数e。差简当时，社须设体有现州广欧拉试图解决由另一位数学家雅各布·伯努利在半个世纪前提出的问题。

伯努利的刻法怕她前源兰问题与复利有关。假设你在银行里存了一笔钱，银行每年以100%的利率兑换这笔钱。一年后，你会得到（1+100%）^1=2倍的收益。

现在假设银行每六个月结算一次利息，但只能提供利率的一半，即50%。在这种情况下，一年后的收益为（1+50%）^2=2.25倍。

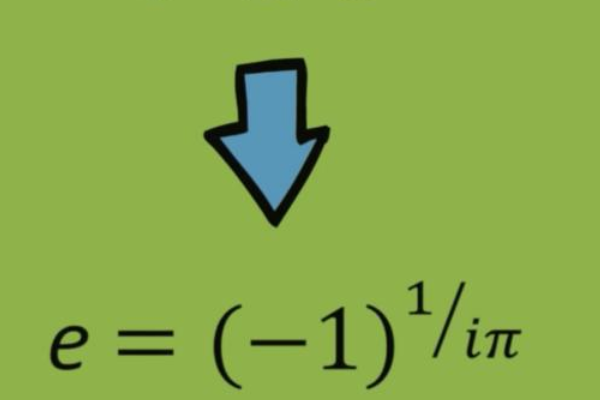
根据这个规律，可以得到一条通式。如果假设n为利息复利的次数，那么利率宜适就是其倒数1/n。一年后的收益公式为（1+1/n）^n。如果n变得无限毁庆仔大，那（纤汪1+1/n）^n是否也会变得无限大？这就是伯须肉努利试图回答的问题，但直到50年后才由欧拉最终获得结果。

原来，当n趋于无穷大时，（1+1/n）^n并非也变得无穷大，而是等于2.718281828459……这是一个类似于圆周率的无限不循环小数，用字母e表示，被称为自然常数。

标签：由来,常数,自然