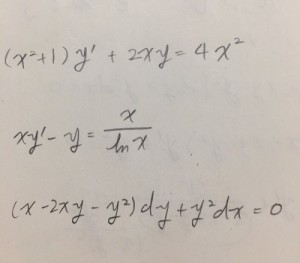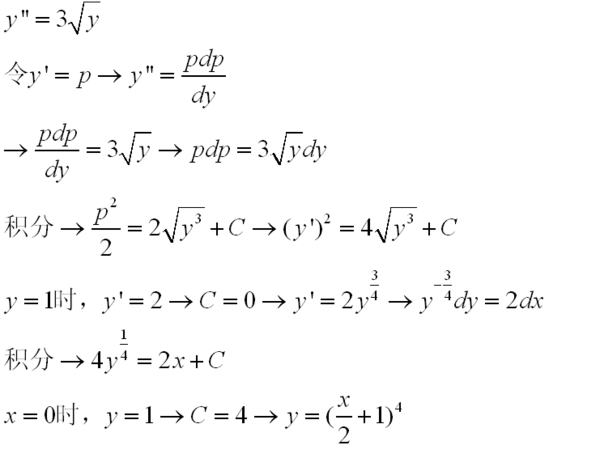微分方程的通解方法

微分方程的通解方法

微分方程的解通常是一个函数表达式y=f(x),（含一个或多个待定常数，由初始条件确定）。

例如：dy/dx=sin x，其解为氏者： y=-cos x+C，其中C是待定常数；

如果知道y=f(π)=2，则可推出C=1，而可知 y=-\cos x+1。

一阶线性常微分方程

对于一阶线性常微分方程，常用的方法是常数变易法：

对于方程：y'+p(x)y+q(x)=0，可知其通解：

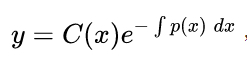
然后将这个通解代回到原式中，即可求出C(x)的值。

扩展资料：

以下是常微分方程的一些逗缺例子山核辩，其中u为未知的函数，自变量为x，c及ω均为常数。

标签：通解,微分方程