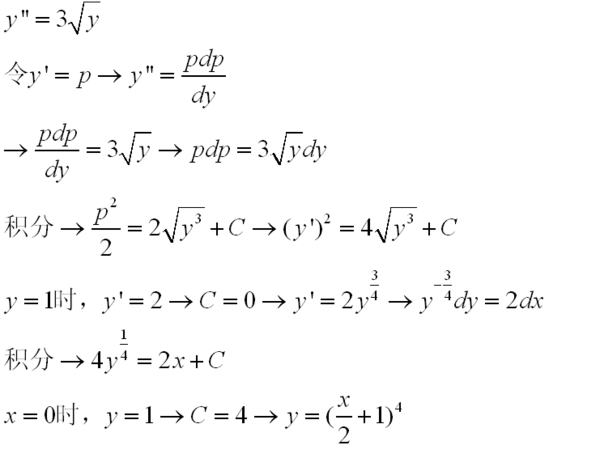微分方程的特解

令z=y/x则y=xz,y'=z+xz'
带入原方程可得:z+xz'=z+tanz
化简得:xz'=tanz=sinz/cosz
即coszdz/sinz=dx/x
即dsinz/sinz=dx/x
即dln|sinz|=dln|x|
积分得:ln|(sinz)/x|=A
即(sinz)/x=±e^{A}=B
即sinz=Bx
z=arcsin(Bx)
即y/x=arcsin(Bx)
y=xarcsin(Bx)
标签:特解,微分方程
版权声明:文章由 酷百书 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.kubaishu.com/life/220974.html