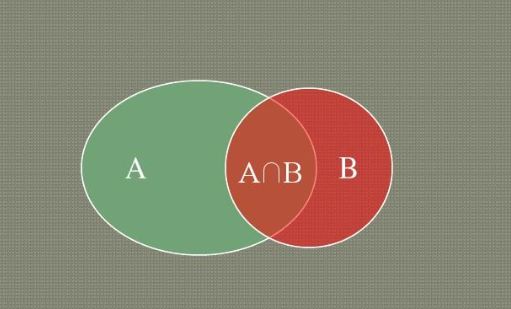
集合间的基本关系有哪些

集合间的基本关系有哪些

1、子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。符号语言：若∀a∈A，均有a∈B，则A⊆B。

2、如果集合A⊆B，存在元素x∈B，且元素x不属于集合A，我们称集合A与集合B有真包含关系，集合A是集合B的真子集（proper subset）。记作A⊊B（或B⊋A），读作“A真包含于B”（或“B真包含A”）。

3、如果两个集合S和T的元素完全相同，则称S与T两个集合相等，记为S=T 。

扩展资料：

集合的特性

1、确定性

给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现。

2、互异性

一个集合中，任何两个元素都认为是不相同的，即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画，可以使用多重集，其中的元素允许出现多次。

3、无序性

一个集合中，每个元素的地位都是相同的，元素之间是无序的。集合上可以定义序关系，定义了序关系后，元素之间就可以按照序关系排序。但就集合本身的特性而言，元素之间没有必然的序。

参考资料来源：搜狗百科-集合

标签：集合,基本