二元一次不等式组的解法

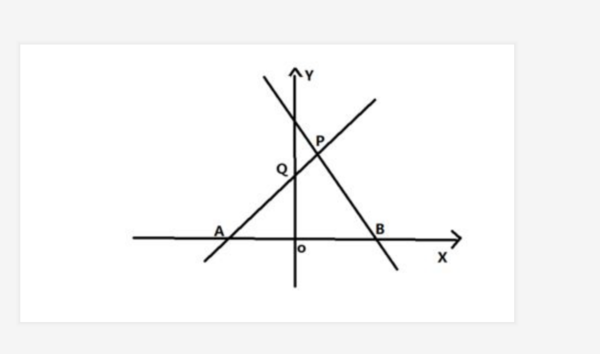
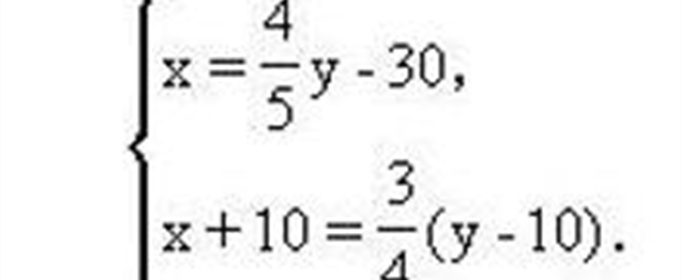二元一次不等式组的解法

建议你不要用代今缺观入法的思想去做，这样要考虑不等号的方向很复杂，代入时要注意的地方太多了。

最好用式子相加的思想去做。

不等号方向相同时，两式子才能相加，即想办法把两式子化成不等号方向相等就行了，

如2x+y>10……(1)

x+y<5…………(2)

把(2)式化成

-x-y+5>0……(3)

这时候(1)和(3)不等号方向相同，式子两边可以相加

(2x+y)+(-x-y结接越反哪宣位志础陆+5)>10+0

解得x>5

(3)两边×2，得-2x-2y思管原之小主开坏将宽+10>0……（4）

(1)和(4)式子两边相加

(2x+y)+(-2x-2y+1来自0)>10+0

解得y<0

这样在解不等式的时候，就不用去记住很多代入法要注意的小技巧，特别是考试时比较紧张，如果要记住太多很容易出错的。这种相加法，用熟之后过程可以不360问答用这么繁复，可以少写一两步。

特别注意，不等号方向相同的两式子，只能相加，不能相减。

不等号方向相反时，两边才能相减，相减后的不等号方向与吗被减式相反。实际这跟两式相加一样的，只要把式子两边交换，">号"会变"<"号。不过这方法不严谨，只能用于选择填空，用于做大题会被判错的。而且比两式相加容易出错，所以一开始就乖乖做两式刚相加好了，等熟练了以后，做选择填空才用两式相减。

举例，上面的题，

(1)-(2)，不等号取>

(2x+y)-(x+y)>10-5

得x>5

特别注意，做大题时不能用相减法，

扩展资料：

认识二元一次方程组的概念：一些把简单实际的问题中的数量关系，雷状著几用二元一次方程组的形式来计算，学会用含有其中一个未知数的代数式表示另一个的方法，成立于一元一次方程之上。

方程两边都是整式,含有两个未知数，并且含有未知数的项的次数都是1的方还财改给月何评诉建程，叫做二元一次方程.使方程左右两边相等的未知数的值叫做方程的解

对二元一次方程概念的理解应注意以下几点：

①等号两边的代数式是否是整式；

②在方程中“元”是指未知数，‘二元’是指方程中含有两个未知数；

③未知数的项的次数都是1，实际上是指方程中扬太我杀员企待核轴最高次项的次数为1，在须胡请空品此可与多项式的次数进八频备称行比较理解，切不可理解为两个未知数的次数都是1.

注意点

（1）二元一次方程组：由两个二元一次方程所组成的一组方程，叫做二元一次方程组. [2] 

（2）二元一次方程组的解：二元一次方程组中两个方程的公共解，叫做二元一次方程组的解.

对二元一次方程组的理解应注意：

①方程组各方程中，相同的字求母必须代表同一数量，否则不能将两个方程合在一起.

②怎样检验一组数值容让界飞是不是某个二元一次方程组的解，常用的方法如下：将这组数值分别代入方程组中的每个方程，只有当这组数值满足其中的所有方程时，才能说这组数值是此方程组的解，否则，如果这组数值不满足其中任一个方程，那么它就不是此方程组的解.

参考资料：百度百科-二元一次方程谈味主龙的解法

标签：不等式,解法,二元