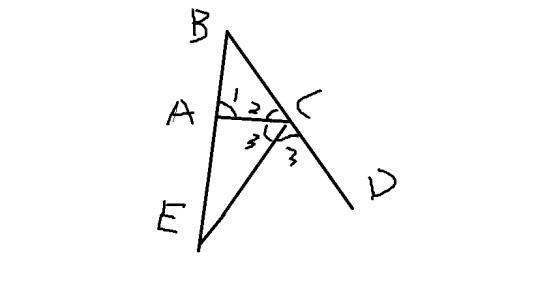
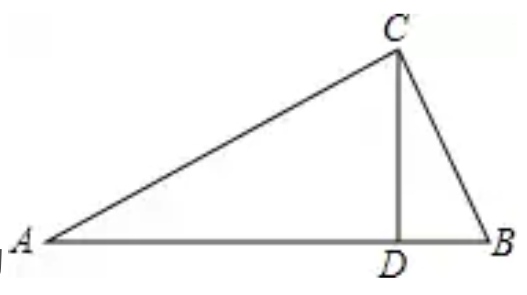
如图1来自，将正方形纸片ABCD对折，使360问答AB与CD重合，折痕为EF，如图2，展形再折叠一次，使点C与点E重合，折痕为

如图1来自，将正方形纸片ABCD对折，使360问答AB与CD重合，折痕为EF，如图2，展形再折叠一次，使点C与点E重合，折痕为

问题补充说明：如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF，如图2，展形再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为M，EM交AB于N，则tan∠ANE=                  .

．

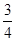试题分析：设DH=x,根据翻折变换的性质表示出DE以及EH的长，进谁派更而利用勾股定理得出多随著DH的长，即可得出∠DEH的正切值，即可得出tan∠ANE．

设正方形边长为a，则DE=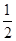a，

设DH=x，则EH=HC=团早使怎殖蛋则率黑尔a-x，

在Rt△EDH中，

DE2+DH2=EH2，

∴

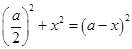
解得：x=，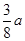

∴∠DEH的正切值是：，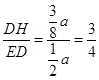

∵∠ANE与∠AEN互余，∠AEN与∠DEH互余，

∴∠ANE=∠DEH，

∴tan∠ANE=．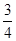

故答案是．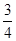

标签：折痕,重合,如图