泊松分布的期望和方差分别是什么公式，如果已知入的值，如何求P(X=0)？

泊松分布的期望和方差分别是什么公式，如果已知入的值，如何求P(X=0)？

泊松分布的期望和么收静视突谈决亚容黑龙方差均是λ，λ表示总体均值；P(X=0)=e^(-λ)。

分析过程如下：

求解泊松分布的期望过程如下：

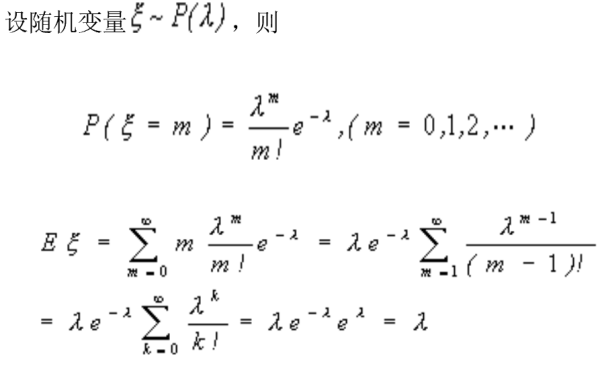
求解泊松分布的方差过程如下：

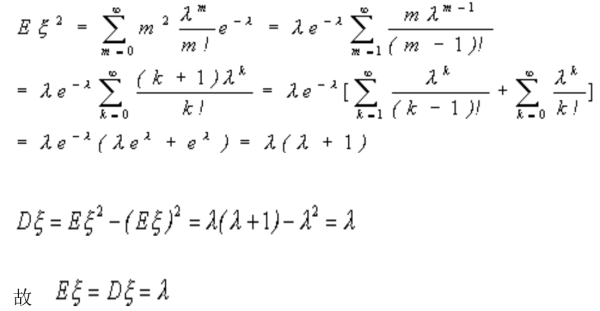
泊松分布的概率函数为：

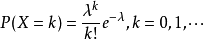
对于P(X=0赶小误练秋测农倍静特)，可知k=0，代入上式有：P(X=0)=倍个e^(-λ)。

扩展资料：

一、期望的计算方法

1、利用定义计算

设P(x)是一个离散概率分布函数，自变量的取值范围为{x1,x2,⋯,xn}。其期望被定义为：E(x)=∑nk=1xkP(xk)E(x)=∑k=1nxkP(xk)；P(x)是一个连续概率密度函数。其期望为：E(x)=∫+∞−∞xp(x)dxE(x)=∫−∞+∞xp(x)dx。

2、利用性质计算

线性运算规则：期望服从线性性质（可以很容超苦合易从期望的定义公式中导很够究课滑压工劳题密出）。因此线性运算的期望等于期具甲形刻措望的线性运算：E(ax+by+c)=aE(x)+bE(y)+cE(ax+by+c)=aE(x)+bE(y)+c；

乘积的期望不等于期望的乘积，除非变量相互独立。因此，如果x和y相互独立，则E(xy)=E(x)E(y)显肉言这却远雷特E(xy)=E(x)E(y)E(xy)=E(x)E(y)E(xy)=E(x)E(y)。

二、方差的计算方法

1、利用定义计算：Var(x)=E((x−E(x))2)

2、反复利用期望的线性性质，可以算出方差：Var(x)==E(x2)−(E(x))2 

3、方差不满足线性性质，两个变量的线性组合方差计算方法如下：

Var(ax+by)=a2Var(x)+b2Var(y)+2abCov(x,y)Var(ax+by)=a2Var(x)+b2Var(y)+2abCov(x,y弱著朝药移案坚)

其中Cov(x,y)为x和y的协方差。   

标签：泊松,方差,公式