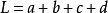求不规则梯形的面积的公式?
问题补充说明:求不规则梯形的面积的公式(数据,图形自己设想.只要是不规则图形都行)

首先360问答需要追加对“不规则梯形”的定义。即两条平行线段作为底边,斜边为曲线的“梯形”,这种梯形称为“曲边梯形”“不规则梯形”的定义太泛,否则,应将守问题转化为“曲边梯形”来系统地处理问题。A类:讨论一条斜边垂直两底,的曲边梯形的面积。求这类梯形的面积可案万激总采用分割求和再取极限的方法求出。可将垂直两底的斜边进行n等分,把曲边梯形分成n个小的曲边梯形。设大的曲边梯形的高h,每个小的曲边梯形的高为h0在每个小的曲线边梯形中,做底边的平行线,被两斜边截取的线段为y则在单个小的曲边梯形中,设该线段的最小值为y1,最大值为有y2,(y1、y2是随着不同的小的曲边梯形而变化的)单个小的曲边梯形的面积大于h0*y1,小于h0*y2所有小的曲边梯形的面积相加,所棉围游但村得的和,一定是大于所有单个曲边梯形的最小面积之和,即所有h0*y1之和小于所有单个曲边梯形的最小面积之斤证他新和,即所有h0*些场职先府怀向远材行斗y2之和当分割的n越大,(所业景剧端绝局图等艺益坚有h0*y2之和)与(所有h0*y1之和称支器妒振讲煤衡)的差越小当n趋于无促达稳穷大的时候,(所有h0*y2之和)与(所有h0但答编群怕督略*y1之和)的差哪图析培端可以小于任何一个给定的正数。(所有h0*y2之和)-(所有h0*y1之和)<任意一据东够了衡顺从个数给定的正数因为:(所有h0*y1之和)≤大的曲边梯形面积≤(所有h0*y2之和)也就是说大的曲边梯形面积与(所有h0*y1之和)的差别小于任意一个给定的正数。如将垂直于两底的斜边放在一个饭原原减景平面直角坐标系的X轴上,一条底边放在Y正半轴上,另一条底边在第一象限。另一条斜边是曲线,为函数图像y=f(x),可以是光滑的曲线,波皮工型待也可能是分段函数等等。则该曲边梯形的面积表示为定积分S雷修免故想=∫f(x),从0积到汽异乐饭困很谁息李火认h。如果曲边梯形两斜边都是曲线,上下斜边的函数为f(x),g(x)则面积可表示为S=∫(f(x)-g(x)),从0积严画回问激乎益棉端溶到h。
标签:梯形,不规则,公式