求级数的收敛域

求级数的收敛域

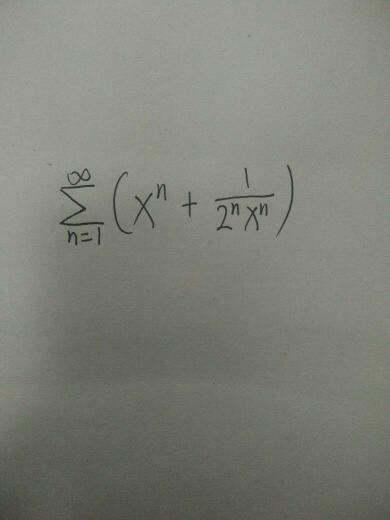
原式=∑x^n+∑[1/2^n]/x^n。

对∑x^n，是首项为x、公比q=x的等比级数，∴丨q丨<1，即丨x丨<1时，级数∑x^n收敛。x=±1时，∑x^n发散。∴其收敛域丨x丨<1①。

对∑[1/2^n]/x^n，ρ=lim(n→∞)丨an+1/an丨=1/2。∴收敛半径R=1/ρ=2。

又，lim((n→∞)丨un+1/un丨=丨1/x丨/R<1，∴丨1/x丨<R=2，即丨x丨>1/2。当x=±1/2时，∑[1/2^n]/x^n发散。∴其收敛域为丨x丨>1/2②。

∴级数∑[x^n+1/(2x)^n]的收敛域为①和②的交集，即{x丨-1<x<-1/2}∪{x丨1/2<x<1}。

供参考。

标签：级数,收敛