什麼是數學建模，數學建模具體要做什麼？
要了解数学建模，首先要知道什么是数学模型。一般地说，数学模型可以描述为，对于现实世界的一个特定对象，为了一个特定目的，根据特有的内在规律，做出一些必要的简化假设，运用适当的数学工具，得到的一个数学结构。而建立数学模型的全过程就称为数学建模。最简单的例子就是，我们中学是做的应用题，通过题目，找出它的规律，列出数学式子，最后解答。数学建模的一般步骤：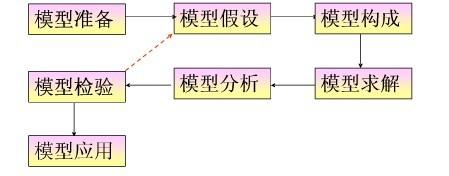 
模型准备——了解问题的实际背景，明确其实际意义，掌握对象的各种信息。用数学语言来描述问题。模型假设——根据实际对象的特征和建模的目的，对问题进行必要的简化，并用精确的语言提出一些恰当的假设。模型建立——在假设的基础上，利用适当的数学工具来刻划各变量之间的数学关系，建立相应的数学结构（尽量用简单的数学工具）。模型求解——利用获取的数据资料，对模型的所有参数做出计算（或近似计算）。模型分析——对所得的结果进行数学上的分析。模型检验——将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合，则要对计算结果给出其实际含义，并进行解释。如果模型与实际吻合较差，则应该修改假设，再次重复建模过程。模型应用——应用方式因问题的性质和建模的目的而异。
标签：什麼,數學,數學建
版权声明：文章由 酷百书 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.kubaishu.com/life/125386.html
