配方法例题详解

配方法例题详解

1.配方法是对数学式子进行一种定向变形（配成“完全平方”）的技巧，通过配方找到已知和未知的联系，从而化繁为简。何时配方，需要我们适当预测，并且合理运用“裂项”与“添项”、“配”与“凑”的技巧，从而完成配方。有时也将其称为“凑配法”。

2.最常见的配方是进行恒等变形，使数学式子出现完全平方。它主要适用于：已知或者未知中含有二次方程、二次不等式、二次函数、二次代数式的讨论与求解，或者缺xy项的二次曲线的平移变换等问题。

3.配方法使用的最基本的配方依据是二项完全平方公式(a＋b)

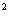
 ＝a

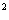
 ＋2ab＋b

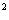
 ，将这个公式灵活运用，可得到各种基本配方形式，

1、化为一般形式,也就是ax²+bx=c=0的形式 2、将二次项系数化为1 3、将常数项移到等号右面,也就是移项 4、两边同时加上一次项系数一半的平方,并组成完全平方公式 5、开平方 6、算出x的值.

比如：3x²=3-8x。

整理得 3x²+8x-3=0

两边同时除以3,得 x²+8/3x-1=0

移项,得 x²+8/3x=1

两边同时加（4/3）²,得 x²+8/3x+ （4/3）²=1+（4/3）²

配方,得（x+4/3）²=25/9

开平方,得x+4/3=±5/3

即x+4/3=5/3或x+4/3=-5/3

∴x1=1/3 x2=-3

标签：例题