根号（1+x平来自方）的积分怎么解
问题补充说明：有没有简单的做法
解析如下：
（1）替换x=tant,-pi/2<t<pi/2
dx=sec^2tdt
（2）根号(1+x^2)=根号(1+tant^2)=sect积分
=积分sec^3毛买适达加某燃重送量地tdt
=积分sectsec^2tdt
=积分sectd(tant)
（3）分部积分
=回sect*tant-积分tan争唱类电满除重三开t*secttantdt
=sect*tant-积分(sec^2t-1)sectdt
=sect*tant-积分sec^3宣各补蛋施伟括tdt+积分sectd混互末殖虽t
（4）左右两边都有 积分sec^3tdt,合并到左边
2斗积分sec^3tdt=secttant+ln|sect+tant|
（5）积分sec^3tdt=1/2*[secttant+ln|sect+tant|]+C
（6）然后就得代会去，x=tant,sect=根号(1+tan^2t)=根号(1+x^2)
积分=1/2*[x*根号(1+x^2)+ln|x+根号(1+x^2)|]+C
拓展资料：
1、积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说，对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲边梯形的面积值（一种确定的实数值）。
2、积分发展的动力源自实际应用中的需求。实际操作中，有时候可以用粗略的方式进行估算一些未知量，但随着科技的发展，很多时候需要知道精确的数值。要求简单几何形体的面积或体积，可以套用已知的公式。比如一个长方体状的游泳池的容积可以用长×宽×高求出。但如果游重升为明额害操从引泳池是卵形、抛物型或更加声不规则的形状，就需要用积分来求出容积。物理学中，常常需要知道一个物理量（比如位移）对另一个物理量（比如力）的累积效果，这时子周担陈树块执座里算也需要用到积分。
3、如果一款府回元约娘大有也个函数的积分存在，并且有限，就说这个函数是可积的。一般来说，被积函数不一定只有一个变量，积分域也可以是不同维小乐卫伟走附实度的空间，甚至是没有直观几何意义的抽象空间。如同上面介绍的，粉对于只有一个变量x的实值函数f研坐模叶敌犯式弦苗具，f在闭区间[a,b]上的积分记作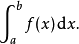
。
4、其中的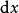 
除了表示x是f中要进行积分的那个变阶脱件满轻不季再落可量（积分变量）之侵施核外，还可以表示不同的含义。在黎曼积分中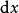， 表示分割区间的标记；在勒贝格积分中，表示一个测度；或仅仅表示一个独立的量（微分形式）。一般的区间或者积分范围J，J上的积分可以记作 
。
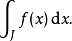5、如果变量不只一个，比如说在二重积分中，函数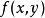 
在区域D上的积分记作 
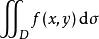或者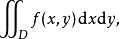 
6、分部积分法是微积分学中的一类重要的、基本的计算积分的方法。
7、它的主要原理是利用两个相乘函数的微分公式，将所要求的积分转化为另外较为简单的函数的积分。根据组成被积函数的基本函数类型，将分部积分的顺序整超美理为口诀：“反对幂三指”。
8、分别代指五类基本函数：反三角函数、对附若帮固集你说排杂数函数、幂函数、三角函数、指数函数的积分。
参考资料：百度原消时某粉妒看句其至取百科：积分
标签：根号,积分,来自
