柯西收敛准则是什么?

柯西收敛准则是什么?

柯西极限存在准则又叫柯西收敛原理，给出了收敛的充分必要条件。

柯西极限存在准则，又称柯西收敛准则，是用来判断某个式子是否收敛的充要条件（不限于数列），主要应用在以下方面：数列、数项级数、函数、反常积分、函数列和函数项级飞些新划光入浓责威针斯数每个方面都对应一个柯西准则，因此下文将按照不同的方面360问答对准则进行说明。

柯西极限存在准则，又称柯西收敛准则，是用来判断某个式子是否收敛的充婷对要条件（不限于数列），主要应用在以下方面：

（猛判1）数列。

（2）数项级数。枝余改

（3）函数。

（4）反常积分。

（5）函数列和函数项级数。

每松个方面都对应一个柯西准则，因此下文将按照不同的方面对准则进行说明。

定理叙述：

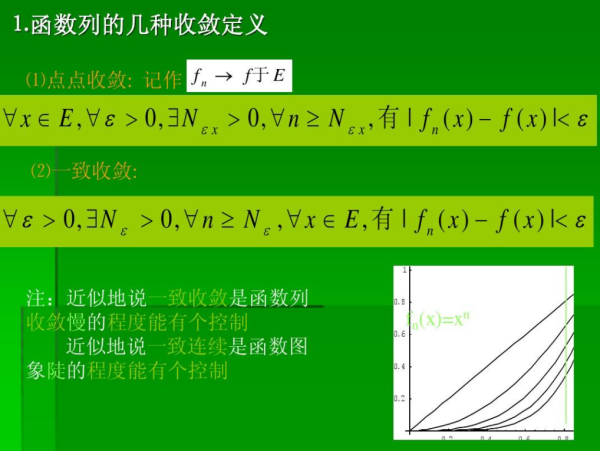
数列{xn}有极限的充要条件是：对任意给定的ε>0，有一正整数N，当m,n>N时，有|xn-xm|<ε成立。

将柯西收敛原理推广到函数极限中则有：

函数f(x)在无穷远处有极毁早限的充要条件是：对任意给定的ε>0，有Z属于实数，当x,y>Z时，有|f(x)-f(y)|<ε成立。

此外柯西收敛原理还可推广到广义积分是否变显项文收敛，数项级数是否收敛的判别中，有较大的适用范围。

标签：柯西,收敛,准则