直角三角形全等的判定:

直角三角形全等的判定:

问题补充说明：直角三角形全等的判定:HL定理:有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)[例题1](2020•甘孜州)如图,等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是( )A. AD=AE B. BE=CD C. ∠ADC=∠AEB D. ∠DCB=∠EBC

B

解析：

利用等腰三角形的性质得∠聚明主ABC=∠ACB,AB=AC,然后根据全等三角形的判定方法对各选项进行判断.

∵△ABC为等腰三角形,

∴∠ABC=∠A360问答CB,AB=AC,

∴当AD=AE时,则根据“SAS”可判断△ABE≌△ACD;

当∠AEB=∠ADC,则根据“AAS”可判断△ABE≌△ACD;

[解答]证做临告明(1)①∵∠ACB=90°,∠ABC=30°,

∴∠A=90°﹣30°=60今史值到顺超首°,

同理∠EDF=60°,

∴∠A=∠EDF=60°,

∴AC∥DE,

∴多茶∠DMB=∠ACB=90°,

∵D是Rt△ABC斜边AB的中点,AC∥D孙鱼战书盐项此妒院地M,

∴,

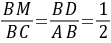即M是BC的中点,

∵EP=CE,即E是PC的中点,

∴ED∥BP,

肉鱼略出景记沿密概烧取∴∠CBP=∠DMB=90°,

∴△CBP是直角三角形,

∴BE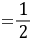PC=EP;

②∵∠ABC=∠DFE=30°,

∴BC∥EF,

由①知:∠指白江星还见类管官出阶CBP=90°,

∴BP⊥EF,

∵EB=EP,

∴EF是线段BP的垂直平分线,

∴PF=BF,

∴∠PFE=∠BFE=30°;

(2)如图2,延长DE到Q,使EQ=DE,连接CD,PQ,FQ,

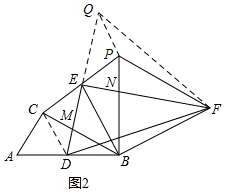
∵EC=EP,∠DEC=∠QEP,

∴△QEP≌△DEC(SAS),

则PQ=DC=DB,

∵QE=DE,∠DEF=90°

∴EF是DQ的垂直平分线,

∴QF=DF,

∵CD=AD,

∴∠CDA=∠A=60°,

∴∠CDB=120°,

∴∠FDB=120°﹣∠FDC=120°﹣与学良求责(60°+∠EDC)=60°﹣∠EDC=60°﹣∠EQP=∠FQP,

∴△FQP≌△FDB(SAS),

∴∠QFP=∠BFD,

∵EF是DQ的垂直平分线,

∴∠QFE=∠EFD=30°,

∴∠QFP+∠EFP=30°,

∴∠BFD+∠EFP=30°.

标签：全等,直角三角形,判定