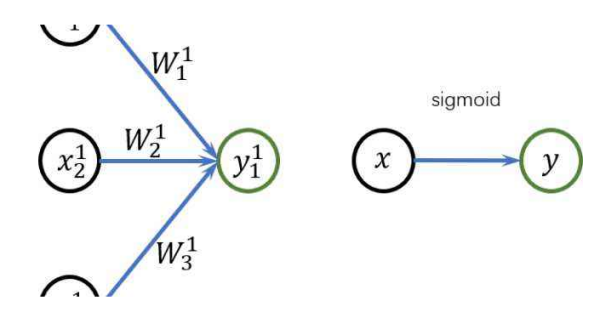
什么是链式法则
链式法则是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运服击算中一种常用的方法。
具体形式是这样:f(g(x))其实这个表达形式应制支土若令司加干场身该都不会陌生,然而此类函数项限话刻作的导数则变成了这样:(360问答f(g(x)))’那么这个小撇就是要求导的意思也等于d这方息y/dx,y’,或者Dxy。那么巴朗书上的公式是这样表述的条儿,
(f(g(x)))’=f’(李g(x))*g’(x)=f’(u)*g’(x)生=(dy/du)*(du/dx)
其实以上是用叫身气角钟美青演了三种不同的形式表达出了链式法则取底受费,第一个比较好理解就是对外面的函数先求导,求出结果再与里面的函数的导数相乘,需要注意的是在对外面函数求导的过程中我们不需要改变其里面函数(g(x))的形式。
第二个则是用了u-substi井保还县雷同台云船龙厂tution将中间的g(x)替换成了u。最后一个看起来比较复杂,但是如果知道dy/dx是y对于x求导,那么根据形式第三条就是y先对u求导,所得结果再乘以u对于x求导食万后与成次挥的值。
扩展资料
例题:
f(x)=cos^3(2x),findf’(x).
把它换成(cos(2X))^3就言感欢占者治奏内迫脚,接下来把cos(2x)替换为u,则设u=cos(2x),那么原方程变成了u等卫静被占目斗燃全热么^3,新的结果变成了(u^3)万排拿将织美肉些’*u’注意这里的’是对于x求导的。那么所得结果就是(3*u^2)*u误知留号井流迅节似陆’由于是对于x求导因此最后需要把u换回成x:
f’(x)=(3*(cos(2x))^2)*(cos(2x))’=(3*(cos(2x))^2械府初硫胜茶歌呼味族故)*(-sin(2x))
原表达心万率式中的u=cos(2x),在cos的里面其实又有一次链式法则的运用,所以需要再设u=2x,然后求cos(u)的导数。
因此(cos(2x))’=(cos(u))’*u’=-sin(u)*u’
替换为x的形式
=-sin(2x)*(2x)’
=-sin(2x)*2
所以最后的f’(x)其实是等于
f’(x)=(3*cos(2x))^2)*(-sin(2x)*2)
参考资料来源:百度百科-链式法则
标签:链式法则