三次函数的对称中心怎么求？详细点，谢谢！比如这个函数 f(x)=ax³+bx²+cx

三次函数的对称中心怎么求？详细点，谢谢！比如这个函数 f(x)=ax³+bx²+cx

求导最为简单，

三次函数的对称中心在函数上,横坐标为-b/3a,

证明：

f(x)=x³+ax²+bx+c

设两个点(-b/3a+t,f(-b/3a+t) ) ,(-b/3a-t,f(-b/3a-t) )

f(-b/3a+t)-f(-b/3a)=at^3+[3a*b^2/9a^2+2b*(-b/3a)+c]t

同理,

f(-b/3a-t)-f(-b/3a)=-at^3-[3a*b^2/9a^2+2b*(-b/3a)+c]t

故f(-b/3a+t)-f(-b/3a)=f(-b/3a-t)-f(-b/3a)

故以(-b/3a,f(-b/3a) )为对称中心。

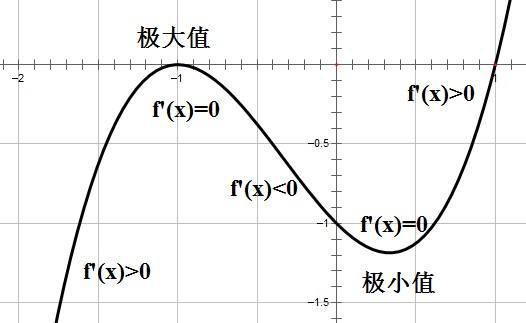
扩展资料：

三次函数极值计算

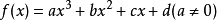
其导数为

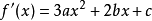
易证当

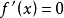
有两个不相等的实数根时，f(x)具有极大值和极小值。而当

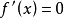
有两个相等的实数根或没有实数根时，f(x)不具有极值。

若f(x)有极值，设在

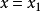
和

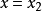
处取得，则满足关系式

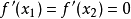
，因此以下用

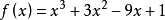
来介绍两种求三次函数极值的方法。

代入原方程法

该方法为高中学生必须掌握的方法，即通过解方程，将所得解x1与x2代入f(x)中得到极值。

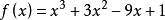
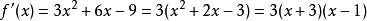
解

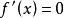
得

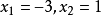
因此极大值：

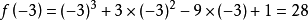
极小值：

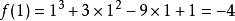
该方法简洁明了，但存在一个问题，即如果解出来的x1与x2十分复杂（如含有根式，或数字较大等），代入f(x)中计算乘方将是一件不容易的事。

参考资料来源：搜狗百科—三次函数

标签：函数,ax,bx