二次型f(x1,x2,x3)=(x1+x2)2+(x2-x3)2+(x3+x1)2的秩为______
二次型f(x1,x2,x3)=(x1+x2)2+(x2-x3)2+(x3+x1)2的秩为2。
解析:
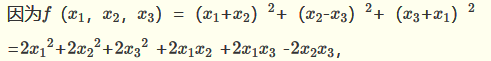
所以二次型的矩阵为:
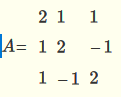
利用初等行变换可得
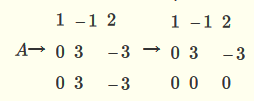
故r(A)=2,即二次型的秩为2。
扩展资料:
二次型的系统研究是从18世纪开始的,它起源于对二次曲线和二次曲面的分类问题的讨论,将二次曲线和二次曲面的方程变形。
选有主轴方向的轴作为坐标轴以简化方程的形状,这个问题是在18世纪引进的。柯西在其著作中给出结论:当方程是标准型时,二次曲面用二次型的符号来进行分类。
二次型化简的进一步研究涉及二次型或行列式的特征方程的概念。特征方程的概念隐含地出现在欧拉的著作中,拉格朗日在其关于线性微分方程组的著作中首先明确地给出了这个概念。
参考资料来源:搜狗百科-二次型
标签:x1,x2,x3
版权声明:文章由 酷百书 整理收集,来源于互联网或者用户投稿,如有侵权,请联系我们,我们会立即处理。如转载请保留本文链接:https://www.kubaishu.com/answer/140407.html


















