黎曼假设的详细内容是什么?蔡塔函数?
黎曼猜想(RH)是关于黎曼ζ函数ζ(s)的零点分布的猜想。黎曼ζ函数在任何复数s ≠ 1上有定义。它在负偶数上也有零点(例如,当s = −2, s = −4, s = −6, ...)。这些零点是“平凡零点”。黎曼猜想关心的是非平凡零点。
黎曼猜想提出:
黎曼ζ函数非平凡零点的实数部份是½即所有的非平凡零点都应该位于直线½ + ti(“临界线”)上。t为一实数,而i为虚数的基本单位。沿临界线的黎曼ζ函数有时通过Z-函数进行研究。它的实零点对应于ζ函数在临界线上的零点。
素数在自然数中的分布问题在纯粹数学和应用数学上都很重要。素数在自然数中的分布并没有简单的规律。黎曼(1826--1866)发现素数出现的频率与黎曼ζ函数紧密相关。
1901年Helge von Koch指出,黎曼猜想与强条件的素数定理
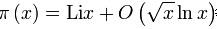
等价。现在已经验证了最初的1,500,000,000个素数对这个定理都成立。但是是否所有的解对此定理都成立,至今尚无人给出证明。
黎曼(1826~1866)观察到,素数的频率紧密相关于一个精心构造的所谓黎曼蔡塔函数z(s)的性态。著名的黎曼假设断言,方程z(s)=0的所有有意义的解都在一条直线上。这点已经对于开始的1,500,000,000个解验证过。证明它对于每一个有意义的解都成立将为围绕素数分布的许多奥秘带来光明。 1730年,欧拉在研究调和级数: Σ1/n=1+1/2+1/3+...+1/n.....。 时,发现: Σ1/n=(1+1/2+1/2^2+...)(1+1/3+1/3^2+...)(1+1/5+1/5^2+...)......=Π(1-1/p)^-1。 其中,n过所有正整数,p过所有素数,但稍加改动便可以使其收敛,将n写成n^s(s>1),即可。如果黎曼假设正确: Π(x)=Li(x)+O(x^1/2*logx) 证明了上式,即证明了黎曼猜想。 在证明素数定理的过程中,黎曼提出了一个论断:Zeta函数的零点都在直线Res(s) =1/2上。他在作了一番努力而未能证明后便放弃了,因为这对他证明素数定理影响不大。但这一问题至今仍然未能解决
标签:蔡塔,黎曼,假设














